Função Quadratica é Par Ou Impar

Função par será uma função par a relação onde o elemento simétrico do conjunto do domínio tiver a mesma imagem no conjunto de chegada.

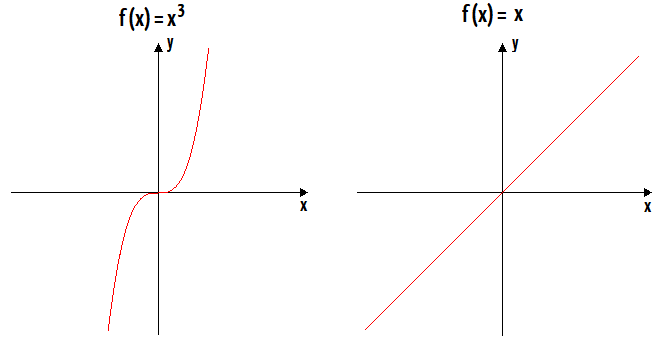
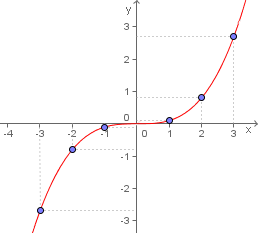
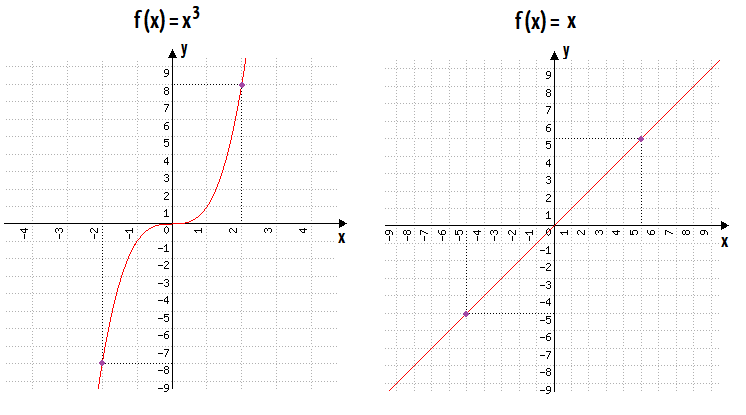
Função quadratica é par ou impar. Como saber se uma função é par ou ímpar. é dita ímpar se a nomenclatura provém do fato que a função é impar se é um número ímpar e par se é um número par. Esses termos se referem à repetição ou simetria da função. Mas nas funções isso não é verdade.

Os valores simétricos devem possuir a mesma imagem. Por isso quando for preciso averiguar se uma função é par através do método algébrico basta substituir x por x e verificar se o resultado é igual ao da função f x inicial. Dada uma função f. Uma função f é par se f x f x.

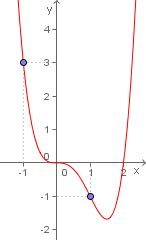
Para que ela fosse uma função ímpar teríamos f x f x ou seja as imagens de x 1 e de x 1 por. Este é um erro muito frequente por parte dos alunos. A melhor forma de saber isso é manipulá la de forma al. Função par estudaremos a forma pela qual se constitui a função f x x 1 representada no gráfico cartesiano note que na função temos.

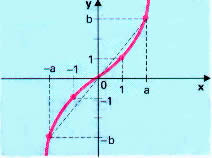
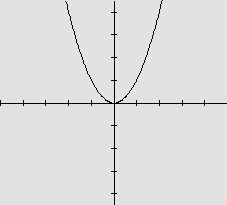
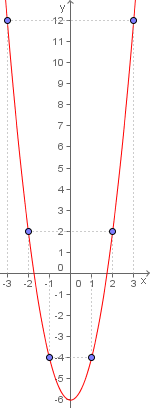
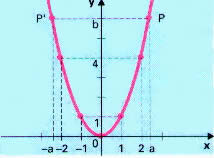
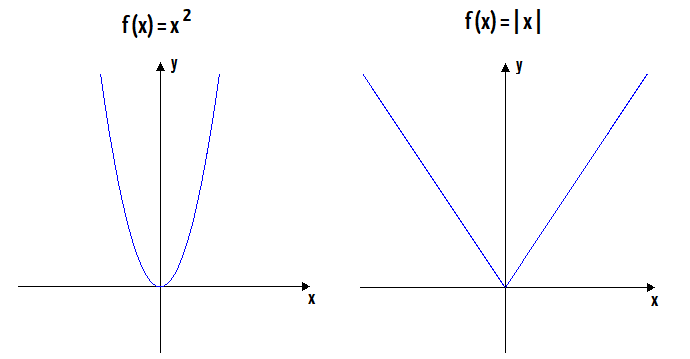
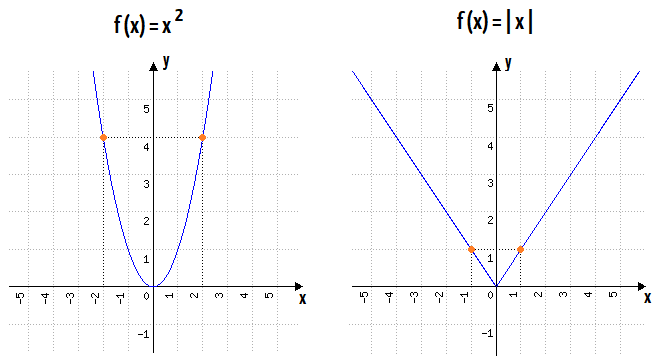
é dita par se uma função. Ir ir definida por f x x 2 é uma função par pois f x x 2 x 2 f x. Existe uma definição totalmente diferente para função par que está explicada num outro tópico. Seja um conjunto com a seguinte propriedade de simetria em relação à origem.

Podemos notar a paridade dessa função observando o seu gráfico. F x x 2. Exemplos é uma função ímpar é uma função par. Função é a relação do conjunto de chegada com o conjunto de partida a forma que assumir essa relação poderá definir uma função como sendo par ou ímpar.

Então pessoal a condição f x f x caracteriza uma função par. Se você concluiu corretamente o gráfico da função estudada na atividade anterior é simétrico em relação ao eixo y no capítulo 3 do módulo 1 vimos que uma curva é simétrica em relação ao eixo y se o ponto x y pertencer à curva sempre que o ponto x y pertencer de acordo com esta observação para que o gráfico de uma função seja simétrico em relação ao eixo y é. Uma forma de classificar funções é defini las como par ímpar ou nenhum dos dois. Então não é uma função par.

A b dizemos que f é par se e somente se f x f x para todo x a. Se um número não é ímpar é porque é par logo se uma função não é ímpar então é par. Saiba identificar uma função par ou ímpar. Ou seja uma função será par se f x.